DOI.ORG/10.58214/VPFU7182
Professor Lorenzo Tancredi discusses the ideas behind the ERC-funded HighPHun project and its proposal to develop a new mathematical language that will potentially open a door to start unravelling the mysteries behind the origin of mass.

Lorenzo Tancredi has led a group on theoretical particle physicists at the Technical University of Munich (TUM) since September 2021. He is mainly interested in mathematical methods in perturbative quantum field theory and their application to collider physics. He has studied at the University of Bologna and at the University of Zurich. He held research positions at the KIT in Karlsruhe and at CERN. In October 2019, he joined the University of Oxford as a Royal Society University Research Fellow.
the concept of mass
We are all intuitively very familiar with the ideas of weight and mass. We all feel ‘very heavy’ when climbing up a steep staircase or carrying home the groceries. We also all know from school that what makes us heavy, and we measure through weight, is what we call the mass of an object. The same volume of different materials can weigh very differently, and we are not surprised if lifting a block of lead feels so much different to a block of polystyrene.
But why is that? Where does the mass of an object come from and how does the mechanism that holds matter together, including every cell in our bodies, depend on this?
These appear to be very basic questions and it might seem almost surprising that, as of today, fundamental physics still does not have a definite answer for them. But let us start from what we do know. In school we learn that all matter is made of atoms. The concept of the atom was invented by the ancient Greeks to indicate what they believed to be the building blocks of matter. In fact, the word atom means ‘indivisible’ or ‘uncuttable’. The Greeks came to this concept without having any experimental proof of it, as at the time the idea of an experiment necessary to demonstrate a theoretical idea did not even exist.
For two millennia this remained just an idea, until the experimental method developed in the 17th Century put in motion one of the most impressive revolutions in human thought: real science was born.
Since then, we have learnt a lot. We could demonstrate that atoms exist, but we also soon learnt that they were not as indivisible as we thought. Atoms are in turn made of smaller objects, or particles. An atom is usually depicted like a miniaturised solar system, with a small and hard core (or nucleus) at the centre, and many smaller particles, the electrons, orbiting around it. While we know today that this picture is somewhat naive, it does convey the main idea well enough. The exact number and pattern of electrons orbiting around the nucleus are very important. They are responsible for all the chemistry and the biology that we know about, including the bonds among carbon atoms that are at the basis of organic chemistry and, therefore, of life as we know it.
Let’s keep this in mind for later and go back to the concept of mass. Most of the atom’s mass is stored in its nucleus, so if we want to understand where it comes from, we must go deeper. The last century, thanks in part to the invention of particle accelerators, has opened our eyes to the inner secrets of atomic nuclei. By colliding particles against each other at increasing energies we have discovered that the nucleus is made of two types of particles: protons and neutrons, which in turn are made of even smaller particles, called quarks and gluons. Protons have a positive electric charge and are the reason why electrons, which have a negative charge, are attracted to fly around them as they do. If you remember the role of electrons in chemistry, this is no little thing. Neutrons instead are, as the name suggests, neutral, they have no charge, and their main role is to act as a glue between protons and keep atomic nuclei together.
Now, as it turns out, the masses of neutrons and protons are very similar but not identical, indeed the proton is a tiny bit lighter than the neutron. In some units that particle physicists like, the mass of the proton weighs 938MeV while that of the neutron 939MeV. This is just a bit more than one per mille difference! Nevertheless, this tiny difference is crucial. In fact, when protons and neutrons are not glued together forming atoms’ nuclei, neutrons being heavier can decay to the lighter protons, losing a bit of their mass emitting an electron and an almost invisible, and very light, (anti-)neutrino. This is a beautiful manifestation of the famous formula discovered by Einstein.
But why is this all important? Oversimplifying things slightly, if the hierarchy of masses were opposite and the proton was a tiny bit heavier than the neutron, the opposite could happen; free protons could decay to neutrons changing everything we know about chemistry that makes life possible as we know it. As you see, a tiny difference in the mass of two particles can make all the difference and the question about its origin is a question about the origin of the universe and of ourselves.

A three-dimensional projection of a Calabi-Yau hypersurface
where is all the mass hidden?
We believe today that the mass of neutrons and protons is determined through a complex mechanism and a large part of it does not come from their individual constituent quarks and gluons. We know protons are made of two types of quarks, two so-called up quarks and one so-called down quark, which are kept together by gluons. Neutrons instead contain two down quarks and one up quark. In the same units in which the proton weighs 938MeV, the up quark weighs around 2MeV and the down quark around 5MeV, while the gluon is massless, just like the photon that makes up the light we see. This means that the total mass of the constituent quarks of a proton is just around 9MeV, while for a neutron is 12MeV, in both cases around 1% of their total mass. The rest of it comes from the energy that keeps quarks and gluons together, once more through Einstein’s . But remember, the difference in the total mass of proton and neutron in the same units was just around 1MeV, which is the same order of magnitude of the mass difference of up and down quarks. Indeed, sophisticated computer simulations have demonstrated that the mass difference between up and down quarks is vital to determine the final mass difference between neutrons and protons. We therefore need to go one step deeper and search for the origin of the mass of quarks.
The value of quarks masses is one of the most fascinating puzzles of modern theoretical physics. Indeed, it turns out that it is not very easy to devise a mathematically consistent way to describe massive particles. The Standard Model of particle physics is the theory that describes how elementary particles (as electrons, photons, quarks, gluons etc) interact with each giving rise to all forces and phenomena that we see around us. It is what we call a gauge Quantum Field Theory. Irrespective of what this complicated name means, the crucial point is that for this theory to make sense, masses cannot exist as simple parameters associated to a particle, but instead they must be generated dynamically through the interaction of elementary particles with the famous Higgs boson. This very elegant solution to the origin of mass was proposed in the 1970s by Higgs, Brout and Englert. It might seem like an artificial solution, and you might be wondering which elements do we have to believe that this theory is the correct one. Well for one thing, the Standard Model predicts some of the properties of elementary particles to almost unbelievable precision. One such property, which has rightfully become famous, is the so-called g-2 of the electron. It is a ‘number’ similar to the mass or the electric charge and it determines how electrons behave in a magnetic field.

A Feynman diagram that describes the production of a pair of top quarks and a Higgs boson at the LHC
You might not believe it, but this property can be measured with 11 digits of precision! Its experimental value reads 0.0011596521807. Now, the same quantity can be computed in the Standard Model. The theoretical calculation up to this precision took 70 years (and there is an ongoing effort in making this calculation even more precise) and the result reads 0.0011596521816. Put the two numbers one under the other and check them. The agreement is simply mindblowing… these numbers are very close, so the Standard Model must be a good theory (even if it is not the ultimate one), and there are many other quantities that have been measured and computed to high precision, finding perfect agreement.
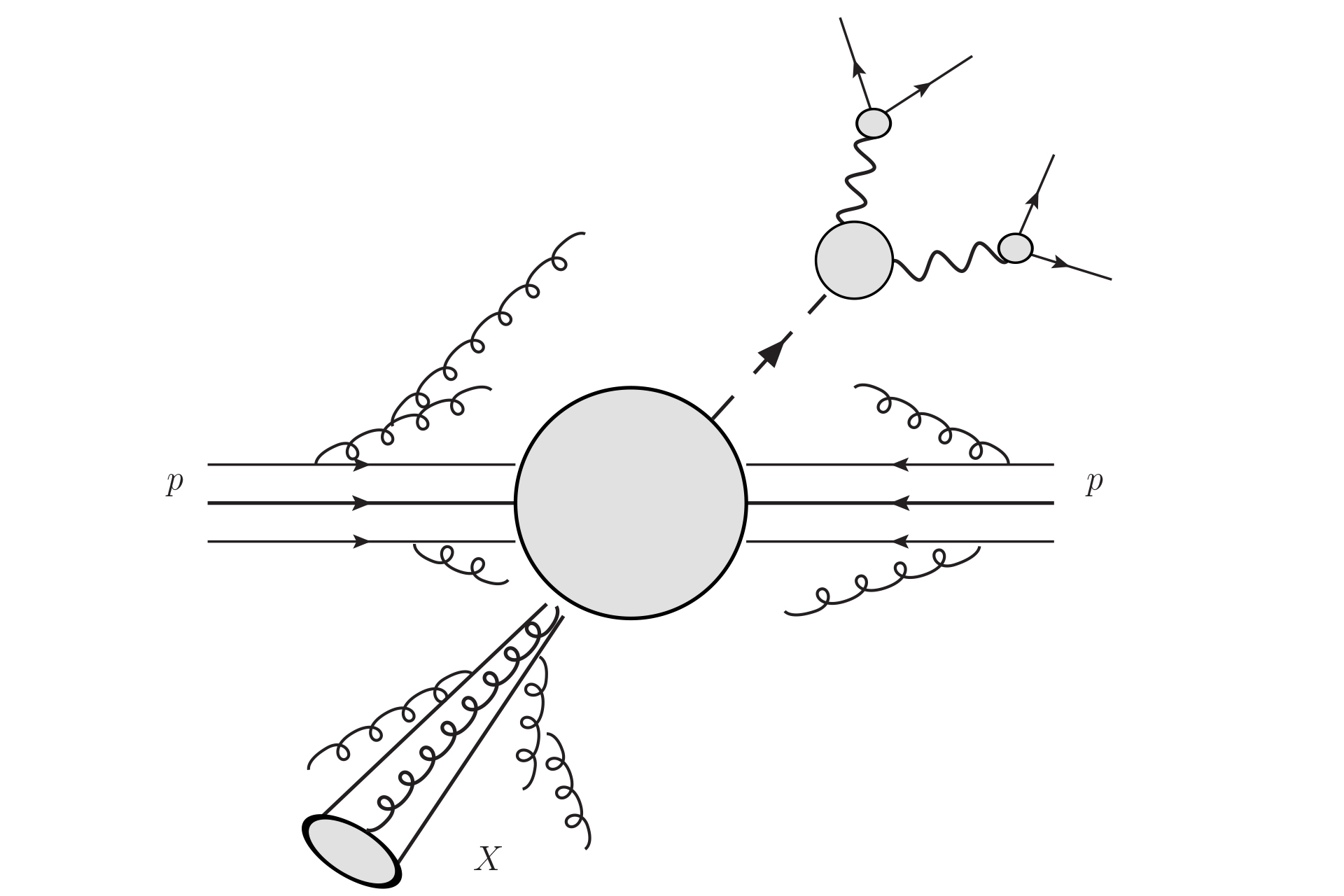
LHC scattering: A graphical representation of the scattering of two protons at the LHC, producing a Higgs boson and a jet of strong interacting particles indicated by X. The three horizontal lines represent the so-called valence quarks in the protons. Curly lines are gluons.
But if these measurements are not enough to convince you, you might have heard that it took us almost 50 years, but in 2012 we were finally able to see the Higgs boson at the Large Hadron Collider (LHC) at CERN, in Geneva, the largest and most powerful particle collider ever built. The discovery of the Higgs boson has been a triumph of theoretical and experimental physics, and one of the most impressive achievements of human thought. It is astonishing that our brains have been able to find the right mathematical framework to describe so much of the behaviour of Nature. If you think about it, it is even more incredible that the language of mathematics, made up by us, can come even close to describing any aspect of any natural phenomena. But then why are we not content yet, what are we still missing?
the missing piece of the puzzle
In the ten years since the discovery of the Higgs boson, the LHC has made more and more precise measurement, providing us with important information about its properties. It does this by colliding protons at very high energy and studying what comes out of the collisions. Among the other things, large numbers of Higgs bosons are produced (again through ), together with many other particles. By measuring precisely the rate at which these particles are produced, the angles at which they fly out of the collision and many other similar observables, we can infer the inner workings of the Higgs boson and of all other particles. While the LHC has been extremely successful and we have learnt a lot, we are still oblivious about the most important question: is it really the Higgs boson that gives masses to all other particles? And what is the mechanism that determines what the hierarchy among these masses are? In fact, in our current formulation of the Standard Model, particle masses enter as parameters that determine how strongly the Higgs boson interacts with them, but their value cannot be predicted theoretically and must instead be inferred by an experimental measurement.
This is very unsatisfactory, in particular given the importance of the tiny difference between up and down quark masses in determining all properties of matter. This becomes even more of a puzzle, if we consider that quarks actually come in three families of two quarks each. Up and down quarks make up the first family, charm and strange the second and top and bottom the third. Up, charm and top quarks are very similar to each other, as are down, strange and bottom. The main difference among them is their mass. Now it turns out that the first family is the only one in which the first quark (the up) is lighter than the second (the down). This hierarchy is inverted in the other two families. This is very intriguing, considering that it is exactly the fact that up quarks are lighter than down quarks that makes atoms stable and life possible! This remains a mystery, but for once we are lucky. Thanks to the LHC and to everything we have learnt about the theoretical foundations of particle physics, all elements to solve this puzzle are now within our reach!
HighPHun: particle physics at the frontier with mathematics
The LHC has discovered the Higgs boson and, in the next 20 years, it will help reveal the details of how the Higgs interacts with all particles, including quarks. The only way we know to make sense of these measurements and extract from them the information we need to determine how particle masses are generated, is to interpret them through precise theoretical calculations for the same quantities. Just as for the electron g-2 discussed above, agreement or disagreement between theory and experiment for different physical observables can teach us which part of our theory is correct and which part needs to be amended and, if we are lucky, give us a hint towards how to amend it. Unfortunately, the precision calculations required for this programme to be successful are extremely complicated and even the largest computers on Earth struggle to give us results at precisions close to those that the LHC will reach in the coming years.

A one-fold Calabi-Yau surface, or a torus
Nevertheless, our efforts in the past two decades have revealed the seeds of a new approach, that could revolutionise the way we address these complex calculations. Indeed, shortly after we started to explore the Standard Model, we have been surprised by the depth of the mathematics involved in its foundation, which largely remain to be understood. What we do know today, is that by digging deep into complex calculations, increasingly rich mathematical and geometrical regularities start to become manifest. They involve in particular types of numbers and functions that appear ubiquitously in apparently unrelated calculations. These numbers and these functions can be seen to be related to special complex geometrical objects, or hypersurfaces, including elliptic curves and so-called Calabi-Yau surfaces. These are nothing but the generalisation of well-known objects such as a sphere or a torus (a doughnut!). These structures turn out to be so important in their own right, that mathematicians have been studying them for decades. The discovery of this profound connection between the theory of particle interactions and special functions attached to the shape of these special hypersurfaces, was one of the most fascinating theoretical discoveries of the first two decades of this millennium.
In fact, we have seen growing evidence of a compelling fact: through studying the details of these geometries we can sometimes find a different path that takes us much more easily to the result of these complicated calculations. Constructing a formalism that allows us to make this connection manifest and understand its implications for arbitrary cases is one of the holy grails for today’s research in theoretical particle physics and is at the heart of the ERC project HighPHun.
Together with my group at the Technical University of Munich, and with international collaborators at the University of Oxford and the University of Bonn, we are working to develop the foundations of this new mathematical language. With it, we will study the properties of the Higgs boson and hope to open a door to start unravelling the mysteries behind the origin of mass.
Professor Lorenzo Tancredi
Professorship on Theoretical Particle Physics
The Technical University of Munich
High Energy Physics at the Frontier with Mathematics (HighPHun)
ERC consolidator grant no. 949279















